Direction Reasoning Questions and Answers
Q-6. A man walks 10km in north and turns right and walks 20km. Again he turns right and walks 50km if he is 20km West from he initial point. Now find that distance how much he walk from initial point.
(a) 35 km
(b) 12 km
(c) 40 km
(d) 10 km
Q-7. A man walking in South direction. After he walks 1 km he turns his right 45° and walks 2 km again he turns his right and walks same distance. Now find that in which direction is he going?
(a) North-West
(b) North-East
(c) South-West
(d) East
Q-8. If South-east becomes North, North-east becomes west and So on that what will west becomes?
(a) North-West
(b) North-East
(c) South-East
(d) West
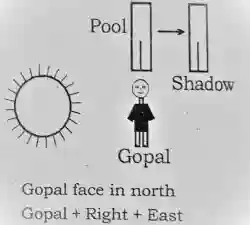
Q-9. An evening Gopal saw a pool . If at the time a pool shadow made his right. Now find that Gopal face which direction?
(a) West
(b) North
(c) South
(d) East
Q-10. Sumit walks 20 m. to the East from point ‘A’, Then walks 20 m. in South-West direction. Then walks 20m in North-West direction and reaches at point B. Find distance b/w A and B.?
(a) O m.
(b) (20√2-1) m
(c) 20 m.
(d) 20√2 m.

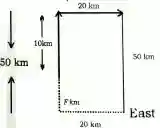 10 + F = 50
F = 50 - 10 = 40 km
10 + F = 50
F = 50 - 10 = 40 km
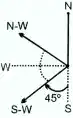 A man is going in South direction from there he turns 45° right means in south west direction and from there right (90°) direction will be north west direction.
A man is going in South direction from there he turns 45° right means in south west direction and from there right (90°) direction will be north west direction.
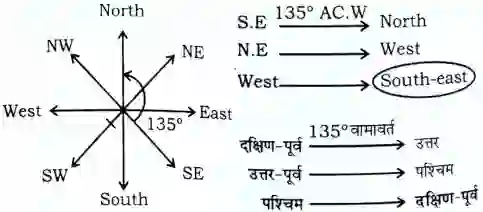 135° AC.W
S.E --------------> North
N.E --------------> West
West.------------> South-east
135° AC.W
S.E --------------> North
N.E --------------> West
West.------------> South-east